2.2仿真数学模型
本文的仿真基于文献[4]中的数学模型。
WLAN接收机接收到的UWB系统设备总的干扰功率可表示为:
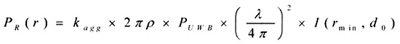 (1)
(1)
其中
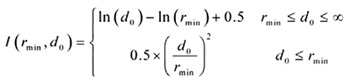 (2)
(2)
kagg为集合因子,综合了环境的影响;PUWB为一个UWB系统用户的发射功率;P为UWB用户的单位密度;λ为中心频率对应的波长;I(rmin,do)是一个传播衰减因素,它由二射线模型得出,决定于rmin、dmin两个参数,rmin是UWB通信设备到WLAN接收机的最小距离;dmin表示拐点。
2.2.1无UWB信号的WLAN系统的信噪比数学模型
在没有UWB信号干扰的情况下,WLAN系统的信噪比表示为:
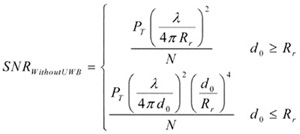 (3)
(3)
其中,PT是在接入点得到的发射功率。
2.2.2存在UWB信号干扰的信噪比数学模型
UWB技术采用短脉冲信号来传送信息,通常每个脉冲持续的时间只有几十皮秒到几纳秒的时间。这些脉冲所占用的带宽甚至高达几GHz,而其设备的发射功率却很小。因此,对于普通的非UWB接收机来说近似于噪声。接收机接收到的总噪声,它由以下几部分组成:
N=No+NF+LIMP(4)
No是热噪声;NL是接收机噪声;LIMP是接收机数字在处理过程中引入的噪声。
在UWB-WLAN共存的模型中,WLAN系统接收到的信号信噪比用dBm来表示为:
 (5)
(5)
PT是在接入点得到的发射功率;Const是路径损耗,它是距离的函数。
图2形象地表示了WLAN系统接收端信号的信噪比SNRmin

图2 WLAN系统接收端信号的信噪比SNRmin
3、仿真结果与分析
3.1无UWB信号干扰的情况下,WLAN系统性能仿真
为了研究UWB系统对WLAN系统造成的干扰,这里首先对没有UWB系统的情况下,WLAN系统的性能参数做了仿真。仿真结果如图3所示。
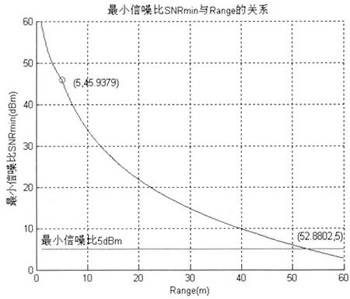
图3 最小信噪比与距离的关系


